The Black-Scholes model, also known as the Black-Scholes-Merton model, is a mathematical framework used in financial markets for the theoretical estimation of the price of derivative investment instruments, such as options and can be calculated in Python. This model was proposed by economists Fischer Black and Myron Scholes, with the contributions of Robert Merton, in 1973.
Derivative instruments, like options, give the holder the right (but not the obligation) to buy or sell an underlying asset (like a stock) at a specific price (the strike price) on or before a specific date (the expiration date). Determining the fair price of these options can be complex, and the Black-Scholes model offers a solution by making some simplifying assumptions about financial markets, including:
- The price of the underlying asset follows a geometric Brownian motion with constant volatility.
- Financial markets are efficient, meaning that the price of the underlying asset reflects all currently available information.
- There are no transaction costs or taxes, and the risk-free interest rate is constant for all maturities.
- The underlying asset does not pay a dividend.
Although these assumptions are oversimplified and often not entirely accurate, the Black-Scholes model is widely used because it provides a relatively simple method for option pricing and it works reasonably well under a variety of conditions. Why and how to calculate Black-Scholes in Python?
Why Implementing Black-Scholes in Python
Python is an excellent choice for implementing the Black-Scholes model for several reasons, especially because of its extensive support for powerful libraries and its strong testing framework. Here’s a more in-depth look at why Python is so well-suited for this task:
- Extensive Library Support: Python provides a variety of libraries that simplify complex mathematical operations, data handling and visualization, all of which can be useful when working with the Black-Scholes model. Here are a few notable ones:
- NumPy: This library supports large, multi-dimensional arrays and matrices, along with a collection of mathematical functions to operate on these arrays. This is particularly useful for operations involving large sets of data, like calculating the price of options with varying parameters.
- SciPy: Built on top of NumPy, SciPy provides additional functionality such as optimization, linear algebra, integration, interpolation, and other applied mathematical techniques. It also includes statistical functions such as the cumulative standard normal distribution function, which is used in the Black-Scholes model.
- Pandas: A library providing high-performance, easy-to-use data structures, and data analysis tools. It’s particularly useful for data manipulation and analysis tasks.
- Matplotlib: This library is used for creating static, animated, and interactive visualizations in Python. It can be used to visualize the output of the Black-Scholes model, such as option prices over time or across different strike prices.
- Ease of Use: Python’s simple syntax makes it easier to write and understand code, which can significantly reduce the time and effort required to implement complex models like Black-Scholes. This simplicity does not compromise its power, making it a great language for both beginners and experienced programmers.
- Testing Frameworks: Python has robust testing frameworks like unittest, pytest, and doctest that allow for both simple and complex automated tests. This is critical for financial models where errors can have significant monetary consequences. With these testing frameworks, you can write tests to ensure that your implementation of the Black-Scholes model behaves as expected.
Without libraries, implementing the Black-Scholes model in Python is still feasible but would require writing a significant amount of code from scratch, including complex mathematical functions like logarithms, exponentiation, square roots, and statistical functions like the cumulative standard normal distribution. This would be more time-consuming, prone to errors, and harder to maintain or understand than using the existing, well-tested, and optimized functions provided by Python’s libraries.
Example of Python Implementation for Black-Scholes
This model assumes that financial markets are efficient and that the price of the underlying asset (such as a stock) follows a geometric Brownian motion with constant volatility. These assumptions are obviously an oversimplification of reality, but the model is still used because it is relatively simple and produces fairly accurate results in many cases.
The formula for the Black-Scholes option pricing model for a non-dividend paying stock is as follows:
C(S, t) = SN(d1) – Xe^-rt*N(d2)
where:
- C = Call option price
- S = Current price of the underlying asset
- t = Time until the expiration of the option
- X = Strike price of the option
- r = Risk-free interest rate
- N = Cumulative standard normal distribution function
- e = Mathematical constant approximated by 2.71828
- d1 and d2 are calculated as:
- d1 = (ln(S/X) + (r + (v^2)/2)t) / vsqrt(t)
- d2 = d1 – v*sqrt(t)
- v = Volatility of the underlying asset
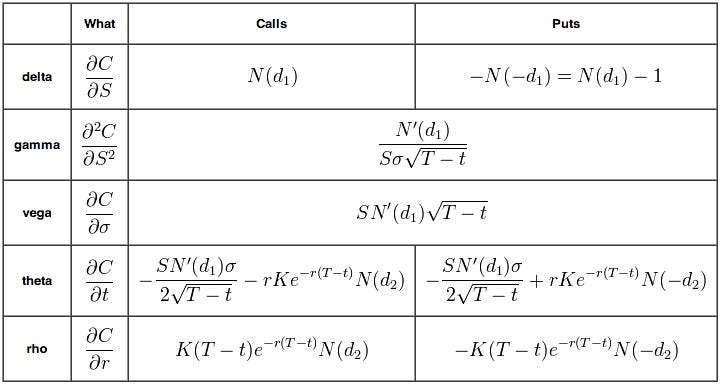
Let’s now translate this into Python code:
import math
import scipy.stats as si
def black_scholes(S, X, t, r, v):
# Calculate d1 and d2 parameters
d1 = (math.log(S / X) + (r + 0.5 * v ** 2) * t) / (v * math.sqrt(t))
d2 = d1 - v * math.sqrt(t)
# Calculate Call Option Price
call = S * si.norm.cdf(d1, 0.0, 1.0) - X * math.exp(-r * t) * si.norm.cdf(d2, 0.0, 1.0)
return call
# Let's test the function with some example parameters
S = 100 # Current price of the underlying asset
X = 110 # Strike price of the option
t = 1 # Time until the expiration of the option
r = 0.05 # Risk-free interest rate
v = 0.2 # Volatility of the underlying asset
call_price = black_scholes(S, X, t, r, v)
print(f"The Call Option price according to the Black-Scholes model is: ${call_price:.2f}")This code defines a black_scholes function that takes as input the current price of the underlying asset, the strike price of the option, the time until expiration, the risk-free interest rate, and the volatility. It uses the math and scipy.stats libraries to calculate the necessary mathematical operations and statistical distributions, respectively. The function returns the price of a European call option according to the Black-Scholes model.
Please note that this implementation only calculates the price for a European call option and does not account for dividends. If you want to calculate the price for a put option or an option on a stock that pays dividends, you would need to adjust the formula accordingly.
Conclusion
the Black-Scholes model is a foundational piece in the world of financial mathematics, offering a theoretical framework for pricing derivative investment instruments like options. While the model’s assumptions do not perfectly reflect the complexities of real-world financial markets, it remains a vital tool due to its relative simplicity and predictive power in many scenarios.
Here is a summary table showing various use-cases for Python implementation of the Black-Scholes model:
| Use Case | Description |
|---|---|
| Option Pricing | The primary use case for the Black-Scholes model is to calculate the theoretical price of European call and put options. |
| Risk Management | The model can help quantify the risk associated with options portfolios, giving insight into potential losses. |
| Trading Strategies | Traders can use the model to identify overpriced or underpriced options, potentially leading to profitable opportunities. |
| Financial Education and Research | The Python implementation can serve as a valuable tool for teaching concepts of financial mathematics and for performing academic research. |
| Automation of Financial Analysis | Python can be used to automate the computation of option prices for large datasets, saving time and reducing errors. |
| Visualization | With libraries like matplotlib, Python can create visualizations of option prices under different conditions, helping users understand the impacts of changes in parameters. |
| Sensitivity Analysis | By tweaking the input parameters of the Black-Scholes model (such as volatility, time to expiration, etc.), one can analyze how sensitive an option’s price is to changes in these parameters. This is useful for understanding and managing the risks associated with options trading. |
| Model Validation | The Python implementation can be used as a baseline to compare with and validate other more complex pricing models. |
Implementing the Black-Scholes model in Python is a practical choice, given Python’s combination of readability, ease of use, and computational power. Python’s extensive libraries such as NumPy, SciPy, pandas, and matplotlib simplify complex mathematical operations, enable efficient data handling, and offer powerful visualization tools, respectively. This makes Python highly effective for financial computations and analysis.
Furthermore, Python’s robust testing frameworks provide a means to ensure the correctness of the implementation and to safeguard against potential errors, which is of utmost importance in financial computations where mistakes can lead to significant monetary losses.
However, as with any model, it’s crucial to understand the assumptions and limitations inherent in the Black-Scholes model. While it provides a good approximation in many cases, it’s not universally applicable. Therefore, it should be used as one of several tools in the decision-making process, supplemented by other models, empirical data, and expert judgment.
The choice of Python as a language for implementing the Black-Scholes model is one that combines academic understanding with practical utility, supporting both the exploration of financial theories and the concrete analysis of financial decisions.

